자료구조 힙에 대한 개념을 알아보고 완전 이진 트리를 통해 최소힙과 최대힙을 구현해보자.
들어가기전에
먼저 힙에 대해 알아보기 전에 완전이진트리의 개념을 상기시킬 필요가 있다. 힙은 완전이진트리의 형태이기 때문이다. 아래의 그림은 포화이진트리를 나타낸 것이다. 포화이진트리는 리프 노드를 제외한 모든 노드들이 2개의 자식 노드들을 갖고있는 트리이다. 포화이진트르의 노드 개수는 높이가 h 일 때 2^(h+1) - 1이 된다.
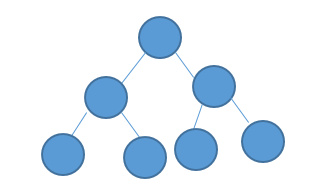
아래의 그림은 완전이진트리를 나타낸 것이다. 위의 포화이진트리에서 가장 오른쪽에 있는 리프노드를 제거한 모습이다. 이처럼 완전이진트리는 왼쪽부터 빈틈없이 채워나간 트리를 의미한다.

아래의 그림은 완전이진트리가 아니다. 왜냐하면 왼쪽 리프노드에 빈 칸이 존재하기 때문이다. 완전이진트리는 반드시 왼쪽부터 순서대로 채워나가야한다.

heap 이란?
힙은 최솟값, 최댓값을 구하는 연산을 빠르게하기 위해 고안된 완전이진트리 형태의 자료구조를 말한다. 또한 완전이진트리에서 부모-자식 노드 간의 규칙이 존재한다. 최소힙일 때는 부모가 자식보다 크기가 항상 작아야 한다. 이러한 규칙을 지킨다면 루트 노드에는 가장 작은 숫자가 저장될 것이다. 반대로 최대힙일 때는 부모가 자식보다 항상 커야 한다.
힙을 활용하여 우선 순위 큐와같은 추상적인 자료형을 구현할 수 있다.
시간복잡도
heap을 통해 삽입과 삭제를 할 때의 시간복잡도는 O(log N)이된다. (이유는 조금 더 공부를 해야할 것 같다.)
최소힙, 최대힙 구현하기
- 힙을 구현하기 위해 리스트를 활용한다.
- n번째 인덱스에 부모노드가 있다면 n * 2와 n * 2 + 1에 자식 노드가 존재한다.
- 위의 인덱스 규칙을 활용하기위해 인덱스 1번부터 활용한다.
class MinHeap():
def __init__(self):
self.heap = [0, ]
# n을 heap의 마지막에 넣은 후에
# heapify를 통해 heap의 형태를 유지하도록 한다.
def push(self, n):
self.heap.append(n)
heap_size = len(self.heap) - 1
self.heapify(heap_size)
# 1번 인덱스에 있는 수를 rseult에 저장하고
# 새로운 heap 리스트에 2번 인덱스부터 옮긴다.
# 새로운 heap 리스트를 heapify를 통해 heap의 형태를 유지하도록 한다.
def pop(self):
result = self.heap[1]
if len(self.heap) >= 3:
self.heap = [0] + self.heap[2: ]
for i in range(len(self.heap) - 1, len(self.heap) // 2 - 1, -1):
self.heapify(i)
else:
self.heap = [0]
return result
def print_heap(self):
print(self.heap)
# 자식 노드의 인덱스를 전달받아 자리를 찾아가게한다.
def heapify(self, child):
parent = child // 2
# 처음 child에 들어온 인덱스의 수가 자기 자신의 자리를 찾을 때까지
# 자신의 부모와 자리를 변경한다.
while parent and self.heap[parent] >= self.heap[child]:
self.heap[parent], self.heap[child] = self.heap[child], self.heap[parent]
child = parent
parent = child // 2
hq = MinHeap()
hq.push(3)
hq.push(4)
hq.push(7)
hq.push(10)
hq.push(2)
hq.pop() # 2
hq.pop() # 3'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 전위 순회와 후위 순회를 알 때의 트리 (0) | 2021.11.11 |
|---|---|
| [자료구조] 스택으로 큐, 큐로 스택 구현하기 (0) | 2021.10.28 |
| [자료구조] 해시 테이블 (0) | 2021.10.21 |
| [자료구조] 트리 : 최소 공통 조상(LCA) (0) | 2021.10.19 |
| [자료구조] 트리의 지름 (0) | 2021.10.14 |