그 동안 알고리즘 문제를 풀 때 dict를 많이 사용하였다. dict는 해시 테이블이라는 자료구조 인데 key-value 쌍으로 데이터를 저장할 수 있다. 원리는 대충 알고있었지만 정확하게 어떠한 원리를 갖고있는지 이해하고 싶어서 정리를 하게 되었다.
해싱
먼저 해싱이라는 개념을 이해할 필요가 있다. 해싱은 랜덤한 길이의 값을 해시 함수를 사용하여 고정된 크기의 값으로 변환하는 것을 의미한다. 아래의 그림과 같이 "apple", "banana", "complete"처럼 문자열의 길이가 다양한 단어가 들어왔을 때 세 자리 정수로 변환하는 작업을 해싱이라 할 수 있다.
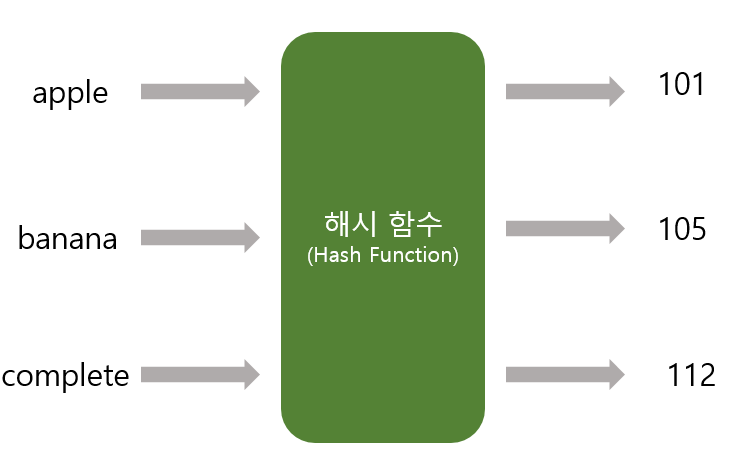
해시 테이블과 해시 함수의 필요성
해시 테이블
해시 테이블은 해시 함수를 통해 변환된 값을 Index로 삼아 Key와 Value를 저장하는 자료구조이다. 해시 테이블은 Key 값을 알고있다면 검색, 삽입, 삭제 연산을 O(1)에 할 수 있다. 하지만 해시 테이블을 효과적으로 사용하기 위해서는 해시 함수의 역할이 중요하다.
해시 함수의 필요성
Key값으로 정수가 주어지고 Key를 인덱스로하여 데이터를 저장해보자. 3과 123을 Key로 갖는 공간에 데이터를 저장한다. 이를 활용하면 Key를 알 때 O(1)으로 검색할 수 있다.
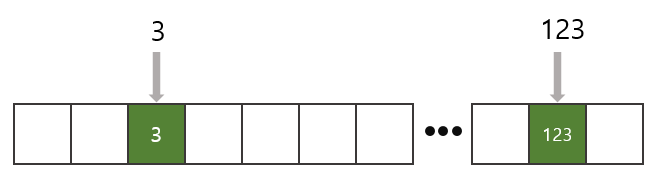
하지만 Key값 중에 미리 설정한 크기보다 큰 정수가 들어온다면 어떻게될까? 이를 대비하여 들어올 Key값 중에 최대 값을 알고있어야 하는 단점이 존재하며 미리 최대 크기로 잡아두었다 하더라도 Key값이 골고루 분포되어있지 않는다면 메모리 낭비가 심할 것이다.
따라서 랜덤하게 들어오는 Key값을 일정한 크기로 변환하는 과정이 필요하기 때문에 해시 함수를 사용하여 해시 테이블에 데이터를 저장하게 된다.
해시 충돌
하지만 해시 함수를 사용하더라도 해시 충돌이라는 문제가 존재한다. Key값을 해시 함수에 넣어 얻은 특정 Index에 데이터를 저장했다. 하지만 이후에 어떤 Key를 해시 함수에 넣어 얻은 Index에 이미 데이터가 존재한다면 충돌이 일어나게 된다. 즉 서로 다른 두 개의 데이터가 같은 Index를 갖게되는 것이다.
이와 같은 해시 충돌을 줄여 해시 테이블을 효율적으로 사용하기 위해서는 해시 테이블의 구조를 개선하는 방법이 존재한다.
해시 테이블의 구조 개선
해시 테이블의 구조 개선을 위해서 Open Addressing과 Chaining 기법이 존재한다.
Open Addressing
개방 주소법(Open Addressing)은 비어있는 해시 테이블의 공간을 활용하는 기법이다. 예를 들어 10이라는 곳에 공간에 이미 데이터가 저장되어있다면 그 다음 위치인 11에 저장을 하는 것이다. 이처럼 개방 주소법의 방법에는 선형 조사법, 이차 조사법, 이중 해시라는 세 가지 방법이 존재한다.
- 선형 조사법
선형 조사법은 가장 기본적인 기법이다. 위에서 설명했듯이 저장하려는 공간에 이미 다른 데이터가 저장되어있다면 한 칸 다음의 위치에 데이터를 저장하는 것이다.
만약 학번에 1000으로 나눈 나머지를 key로 사용하였을 때 2020103과 2019103인 학생의 key가 중복된다고 해보자. 먼저 2019103인 학생이 key를 103으로 하여 데이터가 저장되었다면 2020103은 key를 103으로 저장하려고 할 때 이미 존재하는 것을 확인 후에 바로 옆 칸인 104에 저장할 수 있을 것이다.
이처럼 중복된 key가 존재할 때 key를 +1씩 증가시켜 바로 옆자리를 key로 설정하는 것을 선형 조사법이라고 한다. 하지만 선형 조사법은 충돌의 횟수가 증가함에 따라서 특정 영역에 데이터가 집중되는 클러스터링 문제가 발생하고 이로인해 검색과 삭제가 느려진다.
- 이차 조사법
선형 조사법을 활용하면 충돌이 발생할 수록 key가 한곳에 집중되고, 이는 충돌이 발생할 확률을 높이게 된다. 그렇다면 바로 옆 칸이 아닌 멀리 떨어져 있는 칸을 key로 설정할 수 있을 것이다. 이를 위해서는 +1한 공간에 데이터를 저장하는 것이 아닌 해당 주소에서 제곱한 공간에 데이터를 저장하는 것이다.
이를 통해 선형 조사법보다 데이터를 골고루 저장하여 검색과 삭제에 효율적일 수 있다. 하지만 초기 해시값이 같을 경우에는 선형 조사법과 마찬가지로 클러스터링 문제가 발생할 수 있다.
- 이중 해싱
이중 해싱은 선형 조사법과 이차 조사법에서 발생하는 클러스터링 문제를 해결하기 위해 도입되었다. 저장하려는 공간에 이미 데이터가 존재했을 때 해당 Key를 특정 숫자인 c로 나눈 나머지에 +1을 하여 다음 위치에 저장을 한다. 이때 +1을 하는 이유는 해시 값이 0이 되는 것을 방지하기 위함이다. 또한 통계적으로 c를 소수로 했을 때 클러스터링 문제가 발생할 확률이 낮다고 한다.
Chaining

Chaining은 특정 Key에 이미 다른 데이터가 저장되었을 때 연결 리스트로 이어서 다음 공간에 데이터를 저장하는 기법이다. 위의 그림을 보면 John Smith를 152에 저장을 하였다. 이후 Sandra Dee를 저장하려고 했을 때 이미 데이터가 저장된 152에 저장하려고 한다. 이때 연결 리스트로 공간을 만들어 해당 Key에 이어진 공간에 데이터를 저장한다.
체이닝을 적용하면 하나의 해쉬값에 다수의 데이터가 저장될 수 있다. 따라서 탐색을 할 때 동일한 해쉬 값으로 묶여있는 데이터를 모두 조사해야하는 단점이 존재한다. 하지만 해쉬 함수를 잘 정의했을 때 충돌 확률이 현저히 낮아진다.
정리
- 해싱은 임의의 크기를 갖는 값을 해시 함수를 사용하여 고정된 크기의 값으로 변환하는 과정을 말한다.
- 해시 테이블은 해시 함수로 변환된 값을 Index로 하여 Key, Value 쌍으로 데이터를 저장하는 자료구조를 말한다.
- 해시 충돌을 피하기 위해 해시 테이블의 구조를 개선할 수 있으며 이때 주소 개방법 또는 체이닝을 사용할 수 있다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 힙(heap) (0) | 2021.11.03 |
|---|---|
| [자료구조] 스택으로 큐, 큐로 스택 구현하기 (0) | 2021.10.28 |
| [자료구조] 트리 : 최소 공통 조상(LCA) (0) | 2021.10.19 |
| [자료구조] 트리의 지름 (0) | 2021.10.14 |
| [자료구조] 트리의 부모 찾기 (0) | 2021.10.14 |